铺垫很多，重点就一个：打包节点（Packing Pair of Nodes）。
解决的问题是 ITE的问题，用的方法是打包节点。
详细点就是：
1.先用现成的方案（Full/Partial都有）构造DFG，比如这样的一个DFG (a图)；
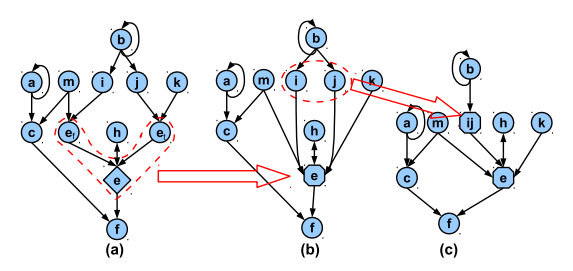
2.有DFG之后用paper里的 Algorithm 1 （输入 DFG D 如上图(a)，输出节点打包后的DFG-节点数量减少（c）)。
算法过程：这是个从后往前推的算法。
# M 是已经打包了的节点的集合，while一直到M不增加，即再没有节点能打包了为止
while |M| increasing do
# C 是候选节点的集合，while到没有候选节点为止
while |C| increasing do
# 这段就是说啥样的节点属于候选节点，遍历 D 里的所有节点，两种节点是候选节点：
# 1. So = So ∩ M -> So 是 o节点的所有后继节点，So = So ∩ M 就是说 So 的所有节点和 已经打包的节点交集都是 So，就是说 o 节点的所有后继都被打包了，这样打包 o节点就不会影响后边的依赖关系了（所以说这个算法得从后往前看，DFG从下到上）；
# 2. o is a select -> 第二种就是 select 节点，整个文章要解决的就是这个 if -else 问题。
for All instructions o in D do
So ← successors of o;
if So = So ∩ M or o is a select then
C ← C ∪ {o};
# 没太明白，大概就是和 clk 有关，得保证这俩节点在一个周期执行才能被打包
ASAP_Schedule D;
ALAP_Schedule D;
# 下边是打包操作，分为两种：
# 1.如果 o 是 select 操作，正中下怀，把 o 和 Ioi 和 Ioe打包成 Po，就是上图DFG (a) 变成 (b)：用六边形 e 打包了 菱形e和 et, ef；
if o is a select instruction then
Pack o, Ioi , and Ioe into Po;
# 2.如果不是 select操作，看if和else的所有输入值（这里 x 表示笛卡尔积），按打包成本排序，i和j成本最低，有共同输入，就打包成 (c)
else
S ← (if-path × else-path) inputs of o;
Sort S by cost of each pair;
if the best cost is positive then
Replace selected pair with Po;
条件
实际也不是有个DFG就框框盲目打包，要先看有没有好处，就是看打包了结点之后对最终 MII(min initiation interval) 有没有改善，别搞了半天结果都一样。
主要看两个因素：
MII = Max(ResMII; RecMII)
RecMII(Recurrence Minimum Initiation Interval): 循环的递归约束引起的II。就是虽然节点可以减少，但是DFG层数和缝没变，下一个cycle插入进来还是不能把II降低，这种情况下白折腾。
ResMII(Resource Minimum II): 硬件资源限制引起的最小II。就是 MxN CGRA，看M，N是多少。
例如：DFG I = (VI, EI ), 有 |VI| 个节点，
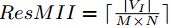DFG节点数除以CGRA PE数向上取整。
需不需要打包节点，得取决于这个值能不能减少，就是看 |VI| 能不能跨越 MxN的边界。
比如DFG有34个节点，即|VI|=34，CGRA是4x4=16个PE，34/16=2.125 -> 3，如果打包后只减少了一个节点，即|VI|=33，那33/16=2.0625 -> 3，最终ResMII还是3，白整。
如果打包后|VI|=32，那32/16=2，就优化了，值得做。
其他一些信息
有3种方法加速有 if-else-then 的loop：Partial Predication/Full Predication/Dual-issue。 Dual-issue 最佳，需要 compiler 支持，这个paper就是弄了个这个compiler。
对比：
- 专用加速器：performance, power-efficiency 都最好，但不能 programmable，有限；
- FPGA灵活，power-efficiency 高；
- GP-GPUs (General-purpose graphics processing units): 因为易于变成和对“parallel loops”的 performence和 power-efficiency好而流行，但只能加速并行循环，因为它的方法是同时执行循环的所有迭代，同时执行非并行循环的迭代不行。
并行loop就是无数据依赖 例如：
// 向量加法 for (int i=0; i<N; i++) { c[i] = A[i] + B[i] } // c[i] 的计算只依赖于 A[i]， B[i]，各次迭代互不干扰可以并行执行
非并行 例如：
// 累加 for (int i=0; i<N; i++) { A[i] = A[i-1] + B[i] } // A[i] 依赖于 A[i-1]，存在顺序，不行
Partial Predication: 不同分支的操作映射到不同的 PE，比如 et, ef，使用 select 合并不同分支的结果；
Full Predication: 更新同一个变量的操作映射在同一个PE。每个分支按顺序（执行顺序）映射到PE，在某个PE上计算condition，得到h：
- 如果h=True，执行 e <- b x X4
- 如果h反=True，执行 e <- b x X5
Dual-issue 和 Full Predication 都靠 predicate 决定分支执行，也是在同一个 PE，不同的是： Full Predication分不同的时钟周期：
if (x > 0) {
y = x + 1
} else {
y = x -1
}
在某一个时钟周期，predicate 决定 y = x + 1 是否执行，在下一个时钟周期决定 y = x - 1是否执行。实际就是只能两个分支挨个判断。
Dual-issue猛就猛在 y = x + 1 和 y = x - 1同时映射到同一个 PE，predicate决定执行哪个，在一个时钟周期就完成了整个条件语句。
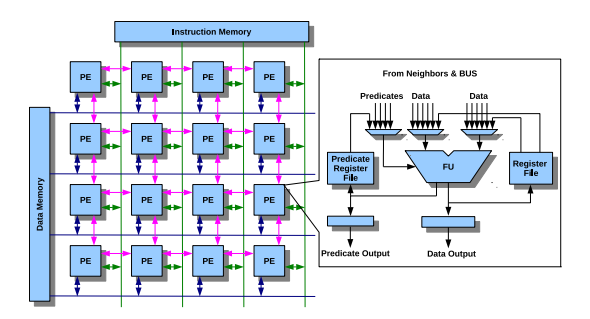
还有个图对理解 PE结构有帮助：
