比如一个kernel如下:
// N = rows*cols
for(int i=0; i<N;++i)
{
int r=i//rows;
int c=i%cols;
out+=mat0[r][c]*mat1[c][r]
}
分析它的数据流图为:
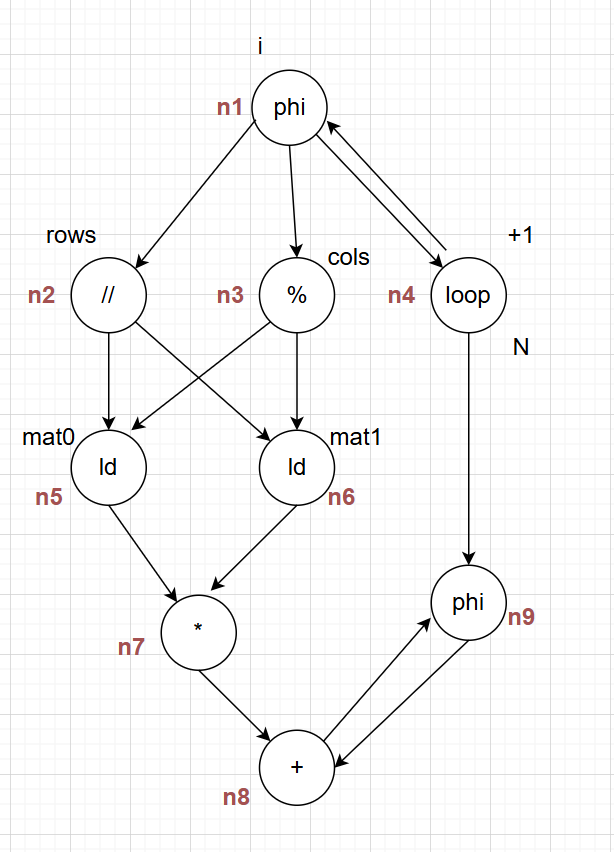
n4:循环+1
n1:判断 i
n2:i // rows
n3:i % cols
n5:接收n2,n3的值并从mat0 load
n6:接收n2,n3的值并从mat1 load
n7:相乘
n8:加法
n9:累加,由n4控制,表示如果满足“i > bound”,则无需进行实际的累加
如果是cpu的话,9个节点,需要9次计算,如果是gpu的话,也要9次计算,但是gpu可以接收向量化计算,就是一次可以计算多个值。
接下来我们看怎么靠一个2x2的cgra来加速计算:
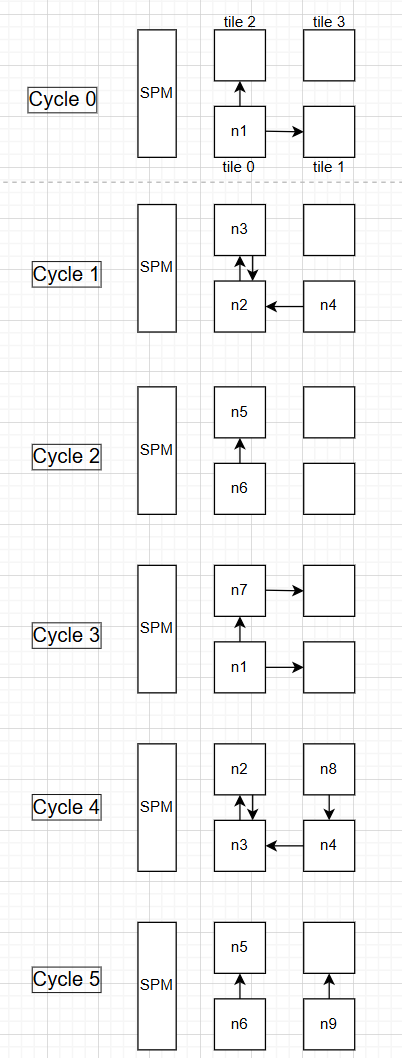
cycle0: tile0计算n1拿到 i,留存在自己mem并输出给tile2
cycle1:tile0用cycle0的 i 算 n2,就是 i//rows,结果存自己mem同时发给tile2,同时tile2用 cycle0的i算n3,就是i%cols,结果存自己mem同时发给tile0,同时tile1可以开始算n4,就是循环+1
cycle2:tile0算n6,即用cycle1的结果加载 `mat1[c][r]`并发给tile2,tile2算n5,即加载`mat0[r][c]`并放在自己mem里
cycle3:tile2算n7,即相乘,然后输出到tile3,同时tile0又可以开始算n1了
cycle4:除了做和cycle1一样的操作,tile3还计算n8,即加法
cycle5:除了做和cycle2一样的操作,tile1还计算n9,out+=累加,并把结果放到tile3供下一次n8使用
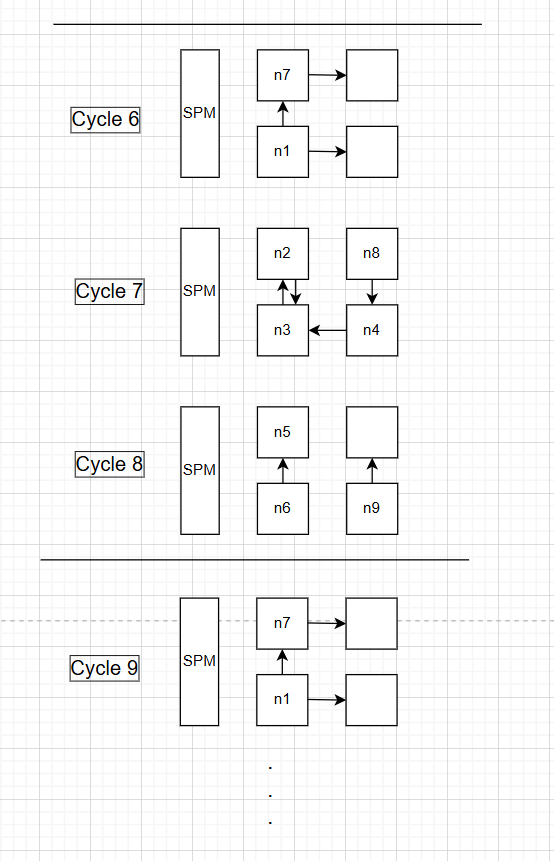
这看似需要5个cycle才能完成一整个计算,但是可以发现从cycle3已经开始流水线了,就是不用完全等到一整个计算结束才开始计算n1,所以等循环跑起来之后,比如下边cycle6 -> cycle8就可以完成n1到n9的所有操作,那么在3个cycle就可以完成一整个操作,II 就是 3。
而cpu/gpu需要9个cycle才能完成,speedup = 9/3 = 3。CGRA加速器实现了cpu/gpu三倍的计算速度。